На практике часто важно изучить зависимости между парами каких-либо переменных. Как можно, например, установить, зависит ли вариация размеров детали от изменений скорости вращения шпинделя токарного станка? Или, допустим, мы хотим управлять концентрацией материала, но предпочитаем заменить измерение концентрации измерением плотности, поскольку на практике ее гораздо легче мерить. Для изучения зависимостей между двумя переменными, такими как скорость вращения шпинделя токарного станка и размер детали (или концентрация и плотность), мы можем воспользоваться так называемой диаграммой рассеивания [1, 8—10].
Диаграмма разброса (рассеивания) — инструмент [1, 8—10, 38—43], позволяющий определить вид и тесноту связи между парами соответствующих переменных.
Эти две переменные х и у могут относиться [1]:
а) к характеристике качества у и к влияющему на нее фактору х;
б) к двум различным характеристикам качества х и у ;
в) к двум факторам х и у, влияющим на одну характеристику качества z.
Для выявления связи между ними и служит диаграмма разброса (рассеивания), которую также часто называют полем корреляции [1]. При выяснении тес ноты связи между парами переменных важно прежде всего построить диаграмму рассеивания и понять ситуацию в целом.
3.6.1. Этапы построения диаграммы разброса (рассеивания)
Можно рекомендовать следующий порядок построения диаграммы разброса (рассеивания) [1, 45].
1. Соберите парные данные (х, у), между которыми вы хотите исследовать зависимость, и расположите их в табл. 3.4. Было бы хорошо иметь по меньшей мере 30 пар данных.
Таблица 3.4
Данные для построения диаграммы разброса (рассеивания)
| X | XI | х2 | ………… | Xi | ………… | Хn-1 | Хn |
| У | У1 | Уг | …………. | Уi | …………. | Уn-1 | Уn |
2. Найдите максимальные и минимальные значения для х и у. Выберите шкалы на горизонтальной и вертикальной осях так, чтобы обе длины рабочих частей осей х и у получились приблизительно одинаковыми (чтобы они уместились на экране компьютера или на стандартном листе бумаги), тогда диаграмму будет легче читать. При определении масштабов возьмите на каждой оси от 3 до 10 градационных делений и при обозначении этих делений используйте (для облегчения чтения) круглые числа. Если одна переменная — фактор, а вторая — характеристика качества, то выберите для фактора горизонтальную ось х, а для характеристики качества — вертикальную ось у.
3. На экране компьютера (на отдельном листе бумаги) начертите график и нанесите на него данные. Если в разных наблюдениях получаются одинаковые значения, покажите эти точки, либо рисуя концентрические кружки, либо нанося вторую точку рядом с первой.
4. Нанесите на диаграмму все необходимые обозначения, например:
а) названии е диаграммы;
б) интервал времени сбора данных;
в) число пар данных;
г) названия и единицы измерения для каждой оси;
д) дата составления диаграммы;
е) имя (и прочие данные) человека, который составлял эту диаграмму. Убедитесь, что перечисленные выше данные, отраженные на диаграмме, понятны любому человеку, а не только тому, кто строил диаграмму.
Типичные виды диаграмм разброса (рассеивания) приведены на рис. 3.8. После построения диаграммы рассеивания необходимо изучить связи между х и V, но для установления силы связи в количественных терминах полезно вычислить коэффициент корреляции в соответствии со следующим определением [1, 45]:
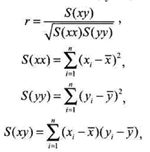
где n — число пар данных; хi, yi — собранные статистические данные; — средние арифметические значения соответствующих факторов х и у; г — коэффициент корреляции, который принимает значение из диапазона -1 ≤ г ≤ 1. Если абсолютное значение г окажется больше 1, то совершенно ясно, что произошла ошибка и вы должны пересчитать результат.
Задание № 3.6.
В таблице приведены данные о давлении воздуха и проценте дефектов при изготовлении пластиковых емкостей. Постройте по этим данным диаграмму разброса (рассеивания).
| Давление, кгс/см2 | Дефекты,
% |
Давление, кгс/см2 | Дефекты,
% |
Давление, кгс/см2 | Дефекты,
% |
Давление, кгс/см2 | Дефекты,
% |
| 9,2 | 0,889 | 8,6 | 0,912 | 8,9 | 0,905 | 9,3 | 0,928 |
| 8,7 | 0,884 | 8,7 | 0,895 | 8,8 | 0,892 | 8,9 | 0,908 |
| 8,4 | 0,874 | 8,5 | 0,896 | 8,8 | 0,877 | 8,9 | 0,886 |
| 8,2 | 0,891 | 9,2 | 0,894 | 8,4 | 0,885 | 8,3 | 0,881 |
| 9,2 | 0,874 | 8,5 | 0,864 | 8,7 | 0,866 | 8,7 | 0,912 |
| 8,7 | 0,886 | 8,3 | 0,922 | 9,2 | 0,896 | 8,9 | 0,904 |
| 9,4 | 0,911 | 8,7 | 0,909 | 8,6 | 0,896 | 8,7 | 0,872 |
Рис. 3.8. Типичные виды диаграмм разброса (рассеивания):
а — сильная положительная корреляция;
б — сильная отрицательная корреляция;
в — слабая положительная корреляция;
г — слабая отрицательная корреляция;
д — криволинейная корреляция;
е — отсутствие корреляции.